个人的变量命名习惯

T test_case
mark 标记
n number
e edge
v vertex
v vector
v volume
v value
w weight
d depth
h head
u/v/w 输入边的起点终点和权重
vis visited
l left
r right
mid middle
pos position
p pointer
s/st start
ed end
m matrix
g graph
s set
q queue
c/cnt count
ans answer
ret return
res result
t/tmp temporary临时变量

数据分析

int的数据范围最高到1e9,超了记得换long long

第二步：构造 tm 结构体

c++

tm t = {0, 0, 0, d, m - 1, y - 1900};

这里用到了 <ctime> 库里定义的结构体 tm，这是 c/c++ 里专门用来表示日期的结构体。

结构如下：

c++

struct tm {
int tm_sec;   // 秒
int tm_min;   // 分
int tm_hour;  // 时
int tm_mday;  // 天
int tm_mon;   // 月（0~11）❗️注意不是 1~12
int tm_year;  // 年（从 1900 开始）❗️
};

所以：

t.tm_mday = d; // 天 = 11
t.tm_mon = m - 1; // 月 = 4 - 1 = 3（代表 4 月）
t.tm_year = y - 1900; // 年 = 2025 - 1900 = 125

第三步：日期 +1 天

c++

t.tm_mday += 1;

直接把天数加 1，可能会超出当前月的天数，比如加到 31 号或 29 号（2 月）等等。

第四步：让系统帮你“进位”

c++

mktime(&t);

mktime 会自动处理你加了一天后产生的 月进位 / 年进位 / 闰年处理。

比如：

2月28日 +1 → 3月1日（非闰年）
2月28日 +1 → 2月29日（闰年）
12月31日 +1 → 下一年 1月1日

算法1-3暴力枚举

P2241统计方形

参考的大佬的题解：https://www.luogu.com.cn/problem/solution/P2241

注意要开long long，因为最坏的情况是从1➕到5000 * 5000，超出了int

等差数列求和公式：

S=n*(n+1) / 2

c++

#include<bits/stdc++.h>

using namespace std;
int n,m;
typedef long long ll;

ll zheng,chang;

int main()
{
    cin >> n >> m;             //对于正方形来说，子矩阵的个数是有原矩阵减去相同的数得到
    for(int i = 0; i < n; i ++)//对于长方形来说，子矩形构成的矩阵的长宽是由原矩形长宽减去不同数而得
        for(int j = 0; j < m;j++)//棋盘中的矩阵不是正方形就是长方形，
        {
            if(i == j) zheng += (n-i)*(m - i);
            else chang += (n-i)*(m-j);
        }
    cout << zheng << " " << chang << endl;
    return 0;
}

P2089烤鸡

题目链接： https://www.luogu.com.cn/problem/P2089

一道比较简单的dfs，这里需要考虑的是最多有几种方案，因为题目说n最大5000，但是从题目意思可知，美味程度最大是30.数据量较小，如果非要说确定的话，3的10次方，最多开6w即可。

c++

#include<bits/stdc++.h>

using namespace std;
int n,ans; //n表示需要的美味程度
int a[10000][10],cmp[10];

void dfs(int id,int degree){//id表示接下来考虑的是哪种配料，degree表示目前的美味程度
    if(id > 10 || degree > n) return;
    
    if(id == 10 && degree == n){
        for(int i = 0; i < 10;i++) a[ans][i] = cmp[i];
        ans++;
    }
    
    for(int i = 1; i <= 3; i ++){
        cmp[id] = i;
        dfs(id + 1,degree + i);//无需恢复现场，因为下次的值会覆盖
    }
}

int main()
{
    cin >> n;
    dfs(0,0);
    cout << ans << endl;
    if(ans){
        for(int i = 0; i < ans ;i++)
        {
            for(int j = 0; j < 10; j ++) cout << a[i][j] << " ";
            cout << endl;
        }
    }
    return 0;
}

P1618三连击

c++

#include<bits/stdc++.h>

using namespace std;
int a,b,c;
int used[10],m[10];//used用来标识数字是否用过，a用来存每一位上放的数字
bool ans = false;
int seg(int w){//w能取1、2、3
    int num = 0;
    for(int i = 3*w - 2;i <= 3*w;i++){
        num *= 10;
        num += m[i]; //就是将对应的前三位，中三位，后三位取出来
    }
    return num;
}

//一共9个数
void dfs(int id){//id表示接下来考虑的是第几位
    if(id > 10) return;
    if(id == 10){
        if(seg(1)*b == seg(2)*a && seg(1)*c == seg(3)*a){
            ans = true;
            cout << seg(1) << " " << seg(2) << " " << seg(3) << endl;
            return;
        }
    }
    
    for(int i = 1; i <= 9;i++){
        if(!used[i]){
            m[id] = i;
            used[i] = 1;
            dfs(id+1);
            used[i] = 0;
        }
    }
}

int main()
{
    cin >> a >> b >> c;
    dfs(1);
    if(!ans){
        cout << "No!!!";
    }
    return 0;
}

P1036选数

该题的关键是选出数的组合不能重复，即位置不同也不行。

如1 、2、3和2、1、3是同一种

因此要设置一个参数来控制选数的顺序，每次选的时候只从他后面选，即可。

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 30;
int q[N],ans,k,n;

bool iszs(int x){
    if(x == 0 || x == 1) return false;
    if(x == 2) return true;
    
    for(int i = 2; i < x;i++){
        if(x % i == 0) return false;
    }
    return true;
}

void dfs(int id,int sum,int order){
    if(id == k){
        if(iszs(sum)) ans++;
        return;
    }
    
    for(int i = order;i < n; i ++)
        dfs(id+1, sum + q[i],i + 1);
}

int main()
{
    cin >> n >> k;
    for(int i = 0; i < n;i++) cin >> q[i];
    dfs(0,0,0);
    cout << ans << endl;
    return 0;
}

P1088火星人

该题的意思就是从给定的一个全排列，顺序往下m个，然后输出他。那么在写的时候按全排列写即可，第一次直接定位到输入的全排列即可

c++

#include<bits/stdc++.h>

using namespace std;

const int N = 10010;
int n, m, ans, flag; //n表示总共几个数排列，m表示要加上的数，ans表示方案数
int a[N];
bool used[N];

void dfs(int u)//接下来考虑第几个数
{
    if(flag == 1) return ;
    if(u > n)
    {
        ans++;
        if(ans == m + 1) 
        {
            for(int i = 1; i <= n; i ++) cout << a[i] << ' ';
            flag = 1;
        }
        return ;    
    }
    
    for(int i = 1; i <= n; i ++)
    {
        if(ans == 0) i = a[u];//将输入的作为排列起点
        if(!used[i])
        {
            a[u] = i;
            used[i] = 1;
            dfs(u + 1);
            a[u] = 0;
            used[i] = 0;
            
        }
    }
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    
    dfs(1);
    return 0;
}

P3799小Y拼木棒

c++

#include<bits/stdc++.h>
#define int long long
        
using namespace std;
const int mod = 1e9 + 7,N = 1e5 + 10;
int num[N];
int n,ans;
        
signed main()
{   
    cin >> n;
    int Min = INT_MAX,Max = INT_MIN;
    for(int i = 0; i < n; i ++) {
        int a;
        cin >> a;
        num[a]++;
        Min = min(Min,a);
        Max = max(Max,a);
    }
    //先选两根相同的，再选出两根使这两根的长度之和与先前选出的相同
    for(int i = Min + 1; i <= Max;i++){
        if(num[i] >= 2){ 
            for(int j = Min; j <= i / 2; j ++){
                if(j != i - j)
                    ans += num[i] * (num[i] - 1) *num[j] * num[i - j] / 2 % mod;//只有之前的两根相同，用公式cn2
                else if(num[j] >= 2 && 2*j == i)
                    ans += num[i] * (num[i] - 1) * num[j] * (num[j] - 1) / 4 % mod;//剩下的两根也想相同
            }
            ans %= mod;//if里只能保证每次加的不超过mod，但是加完之后ans可能超过，因此要mod
        }
    }
    cout << ans << endl;
}

P1044栈

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 20;
int a[2*N][N];
int n;

int dfs(int k,int num){//k表示当前是第几次操作，num表示当前栈内元素个数
    int t = 0;
    if(k == 2*n){
        if(num == 0) return 1;//是合法序列
        else return 0;//不是合法序列
    }
    if(a[k][num] != 0) return a[k][num];//如果之前计算过,直接返回  
    if(num < n) t += dfs(k + 1,num + 1); //栈未满可以push
    if(num > 0) t += dfs(k + 1,num - 1); //栈内有元素可pop
    a[k][num] += t;//记录当前状态的计算结果
    return t; //当前k,num状态下,有多少种合法序列#include<bits/stdc++.h>

using namespace std;
const int N = 20;
int a[2*N][N];
int n;

int dfs(int k,int num){//k表示当前是第几次操作，num表示当前栈内元素个数
    int t = 0;
    if(k == 2*n){
        if(num == 0) return 1;//是合法序列
        else return 0;//不是合法序列
    }
    if(a[k][num] != 0) return a[k][num];//如果之前计算过,直接返回  
    if(num < n) t += dfs(k + 1,num + 1); //栈未满可以push
    if(num > 0) t += dfs(k + 1,num - 1); //栈内有元素可pop
    a[k][num] += t;//记录当前状态的计算结果
    return t; //当前k,num状态下,有多少种合法序列
}
int main()
{
    cin >> n;
    cout << dfs(0,0);
    return 0;
}
}
int main()
{
    cin >> n;
    cout << dfs(0,0);
    return 0;
}

写递归的要点

明白一个函数的作用并相信它能完成这个任务，千万不要跳进这个函数里面企图探究更多细节， 否则就会陷入无穷的细节无法自拔，人脑能压几个栈啊。

算法1-4递推与递归

P1464记忆化搜索

c++

#include<bits/stdc++.h>

using namespace std;
#define int long long

int d[25][25][25];

int w(int a,int b,int c){
    if(a <= 0 || b <= 0 || c <= 0) return 1;
    if(a > 20 || b > 20 || c > 20) return w(20,20,20);
    if(a < b && b < c )
    {
        if(!d[a][b][c-1]) d[a][b][c-1] = w(a,b,c-1);
        if(!d[a][b-1][c-1]) d[a][b-1][c-1] = w(a,b-1,c-1);
        if(!d[a][b-1][c]) d[a][b-1][c] = w(a,b-1,c);
        d[a][b][c] = d[a][b][c-1] + d[a][b-1][c-1] -  d[a][b-1][c];
    }else{
        if(!d[a-1][b][c]) d[a-1][b][c] = w(a-1,b,c);
        if(!d[a-1][b-1][c]) d[a-1][b-1][c] = w(a-1,b-1,c);
        if(!d[a-1][b][c-1]) d[a-1][b][c-1] = w(a-1,b,c-1);
        if(!d[a-1][b-1][c-1]) d[a-1][b-1][c-1] = w(a-1,b-1,c-1);
        d[a][b][c] = d[a-1][b][c] + d[a-1][b-1][c] + d[a-1][b][c-1] - d[a-1][b-1][c-1];
    }   
    return d[a][b][c];
}

signed main()
{
    int a,b,c;
    while(scanf("%lld%lld%lld",&a,&b,&c)){
        if(a == -1 && b == -1 && c == -1) break;
        int ans = w(a,b,c);
        printf("w(%lld, %lld, %lld) = %lld\n",a,b,c,ans);
    }
    return 0;
}

P1928 外星密码

c++

#include <bits/stdc++.h>

using namespace std;

string dg() { // 解压缩函数
    int k;//压缩的次数
    char ch;//输入的字符
    string s = "", str = "";//s是最终答案，str是被压缩的字串
    
    //cin >> ch 会跳过空格和换行符
    while (cin.get(ch)) { //用cin.get()读取字符,避免跳过空格和换行
        if (ch == '[') {//如果找到了被压缩的字串
            cin >> k; // 读取压缩次数
            str = dg(); // 递归调用
            while (k--) {
                s += str;//把解压后的字串复制k次后添加到原来的字符串上
            }
        } else if (ch == ']') {//如果找到了压缩的字串的末尾
            return s; // 结束这一层递归并返回已经解压的字符串
        } else {
            s += ch;//直接在最后添上这个字符。
        }
    }
    
    return s; // 确保函数有返回值
}

int main() {
    cout << dg();
    return 0;
}

P1255 数楼梯

c++

#include<bits/stdc++.h>

using namespace std;
int n,len = 1,arr[5010][5010];//arr[k][i]第k阶台阶所对应的走法,len表示位数 

void highadd(int k)//第k阶台阶,高精度加法 
{
    for(int i = 1; i <= len; i ++)
        arr[k][i] = arr[k-1][i] + arr[k-2][i];//第k阶的方法等于一次走一步+一次性走两步的 
        
    for(int i = 1; i <= len; i ++)
    {
        if(arr[k][i] >= 10)
        {
            arr[k][i+ 1] += arr[k][i] / 10;//进位
            arr[k][i] %= 10;
            if(arr[k][len + 1] != 0) len++;//如果最高位有进位，那么位数➕➕
        }
     } 
 } 

int main()
{
    cin >> n;
    arr[1][1] = 1, arr[2][1] = 2;//初始化
    
    for(int i = 3; i <= n; i ++)//从3开始避免越界 
        highadd(i);
        
    for(int i = len; i >= 1; i --) cout << arr[n][i]; ////逆序输出  
    return 0;
    
 }

P2437 蜜蜂路线

和数楼梯思路一样，只不过要上的阶数是n-m。

P1164 小A点菜

暴力dfs版本(果然TLE了)

c++

#include<bits/stdc++.h>

using namespace std;

int f[110];//存储菜的价格
int n,m,used[110],ans;

void dfs(int id,int num){//id表示当前考虑的是第几个菜品，num表示当前的菜钱
    if(id == n)
    {
        if(num == m) ans++;
        return;
    }
    
    dfs(id+1,num + f[id]);//直接dfs会超时
    dfs(id+1,num);
}

int main()
{
    cin >> n >> m;
    for(int i = 0; i < n; i ++) cin >> f[i];
    dfs(0,0);
    cout << ans;
    return 0;
}

动态规划正解

这是一道简单的动规题，定义f[i]j为用前i道菜用光j元钱的办法总数，其状态转移方程如下：

（1）if(j==第i道菜的价格)f[i]j=f[i-1]j+1;

（2）if(j>第i道菜的价格) f[i]j=f[i-1]j+f[i-1]j-第i道菜的价格;

（3）if(j<第i道菜的价格) f[i]j=f[i-1]j;

说的简单一些，这三个方程，每一个都是在吃与不吃之间抉择。若钱充足，办法总数就等于吃这道菜的办法数与不吃这道菜的办法数之和；若不充足，办法总数就只能承袭吃前i-1道菜的办法总数。依次递推，在最后，我们只要输出f[n]m的值即可。

c++

#include<bits/stdc++.h>

using namespace std;
int f[110][10010];//f[i][j]表示前i道菜(包括第i道),花费j元的方案数
int a[110];//存储菜的单价

int main()
{
    int n,m;
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++){//每种的方案数等于前i-1种选与不选的方案数之和
            if(j > a[i]) f[i][j] = f[i-1][j] + f[i-1][j - a[i]];
            else if(j == a[i]) f[i][j] = f[i-1][j] + 1;
            else f[i][j] = f[i-1][j];
        }
    cout << f[n][m];
    return 0;
}

P1990 覆盖墙壁

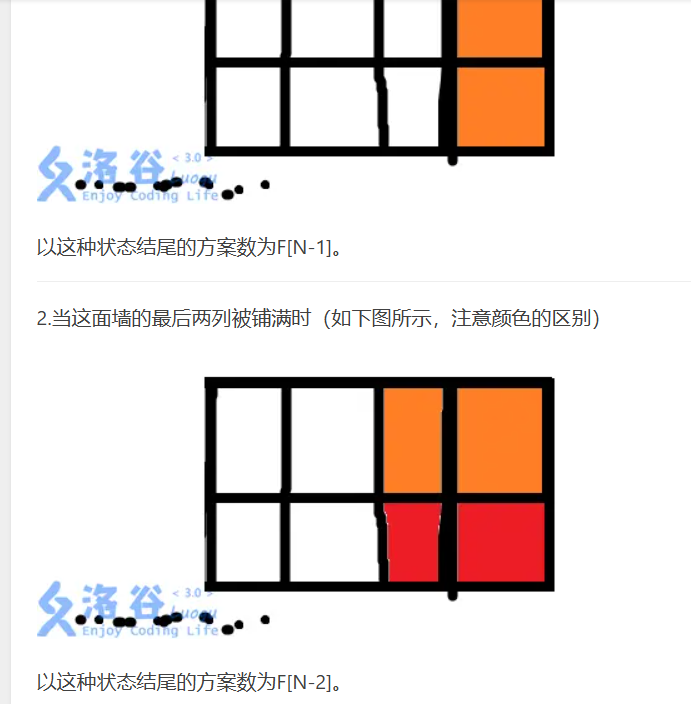
GN：铺满前 N 列墙，且第 N+1列有一个单元被覆盖的方案数，且不考虑第N+1列的格子是上还是下！！

F2=2,F2 = F1+F0+2*G0, F1 = 1, F0 = 1，所以G0 = 0，又因为G1 = F0 + G0,所以G1 = 1. F0 = 1即什么都不放也是一种方案。

FN表示铺满前N*2的面积的墙的方案数.

FN的转移方程就是：

FN=FN-1+FN-2+2*GN-2（别忘了前面讲过GN-2的情况有两种）

而GN的转移方程就是：GN=FN-1+GN-1。

初始化：F0=1,G0=0;F1=G1=1;

但是，L形的瓷砖又怎么办呢？

~~（呵呵，刚开始想到这里的时候，我自己都蒙了。）~~

为了方便大家思考，我们先往简单的方向想。（以下是重点！！！）

我们可以用一个数组GN来表示**铺满前(N+1)*2的面积的墙，但是第(N+1)列有一个瓷砖已经被铺过（注意，是已经被铺过！）**的方案数。

所以，L形瓷砖的问题就已经被“初步”解决了。

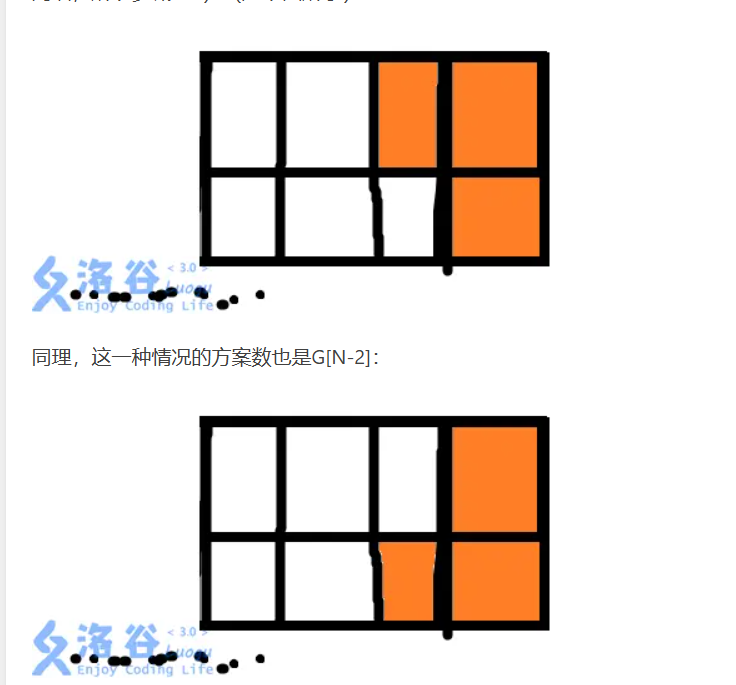
所以，下面这种情况的方案数就是GN-2（因为实际上第N列已经铺满了，所以这里要处理的是前N-1列墙，所以多减了1）（如下图所示）:

c++

#include<bits/stdc++.h>

using namespace std;
const int mod = 10000, N = 1e6 + 10;
int f[N],g[N];

int main()
{
    int n;
    cin >> n;
    f[0] = 1;
    f[1] = g[1] = 1;
    for(int i = 2; i <= n; i ++){
        f[i] = (f[i-1] + f[i-2] + 2*g[i-2]) % mod;
        g[i] = (g[i-1] + f[i-1]) % mod; 
    }
    cout << f[n];
    return 0;
}

P3612 Secret cow code S

先看样例

cOW*−>cOW WcO−>*cOWWcO OcOWWc

我们把这三个字符串编号为1,2,3

现在我们要求第8位，假如我们已经知道在3串，能否逆推出在第2串中的位置呢?如果能，似乎问题就迎刃而解了,因为2逆推到1也是一个相同的子问题。

题目的古怪要求复制要先复制最后一个字符，再复制前缀，我们姑且先直接复制前缀.

cOW−>cOW cOW*−>*cOWcOW cOWcOW

现在求3串的8位置，3串长L,逆推回2串即为8−L/2位置

但我们复制的时候是先复制最后一个字符,所以要多减一为8−1−L/2

特别的,如果求的n刚好是先复制原串的最后一个位置,特殊处理

因为如果是原串的最后一个位置，假设原串长为L，则复制后的串为2L，若位置x - L / 2 - 1 == 0 即是原串的最后一个位置，则将他赋值为i

c++

#include <bits/stdc++.h>
using namespace std;
string s;
long long n,num,i;
int main()
{
    cin>>s>>n;
    num=s.length(); //求出原串的长度
    while(num<n)//n表示要求字符的位置
    {
        i=num;
        while(n>i)  i*=2;//求出当前刚好包括n位置的串长 
        i=i/2;//得到当前串的一半长 
        
        n-=(i+1); 
        if(n==0)    n=i;//即上一个串的最后一个位置
    }
    cout<<s[n-1];
    return 0;
}

P1259 黑白棋子的移动

最左边的o*与空位交换然后空位再和最右边连续**的最后**两个交换

但是注意当o*与空位交换之后，连续的白棋只剩三个的时候规律发生了变化，此时直接打表。

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 210;
char a[N];
int n;
string db[4] = {"ooo*o**--*", "o--*o**oo*", "o*o*o*--o*", "--o*o*o*o*"};//无规律的

void out()
{
    for(int i = 1; i <= 2*n+2;i++) cout << a[i];
    cout << endl;
}

void move(int start,int endi)
{
    swap(a[start],a[endi]);
    swap(a[start+1],a[endi+1]);
    out();
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n;i++) a[i] = 'o';
    for(int i = n+1; i <= 2*n;i++) a[i] = '*';
    a[2*n + 1] = a[2*n + 2] = '-';
    
    out();//输出起始序列
    int len = n;//需要移动的黑/白棋
    while(true)
    {
        move(len,2*len + 1);//空位和o*交换
        len--;
        if(len == 3) break;
        move(len + 1,2*len + 1);
    }
    string ss;
    for (int i = 0; i < n - 4; i++)
        ss += "o*";
    for (int i = 0; i < 4; i++)
        cout << db[i] << ss << endl;
    return 0;
}

P1010幂次方

c++

#include<bits/stdc++.h>

using namespace std;
int n;

void recur(int x)//分解x使其表示为2和2(0)的组合
{
    for(int i = 14; i >= 0;i--)
    {
        if(pow(2,i) <= x)
        {
            if(i == 1) cout << "2";//2(1)不用再往后分解了且2^1输出为2,单独出来
            else if(i == 0) cout << "2(0)";//2(0)也不用再往后分解了,单独出来
            else{//指数不是这两种情况则还得分解
                cout <<"2(";
                recur(i);
                cout << ")";
            }
            x -= pow(2,i);
            if(x != 0) cout << "+";//加号处理的最简单方法:若此x还没分解完,则后面还有项,所以输出一个+号
            
        }
    }
}

int main()
{
    cin >> n;
    recur(n);
    return 0;
}

P1228 地毯填补问题

棋盘是如何划分的：

设当前棋盘的左上角坐标为 (a, b)，边长为 l。
该棋盘被划分成四个 l/2 × l/2 的小棋盘：
- 左上角子棋盘范围： 横坐标： [a, a + l/2 - 1]纵坐标： [b, b + l/2 - 1]
- 右上角子棋盘范围： 横坐标： [a, a + l/2 - 1]纵坐标： [b + l/2, b + l - 1]
- 左下角子棋盘范围： 横坐标： [a + l/2, a + l - 1]纵坐标： [b, b + l/2 - 1]
- 右下角子棋盘范围： 横坐标： [a + l/2, a + l - 1]纵坐标： [b + l/2, b + l - 1]

void dfs(ll x, ll y, ll a,ll b, ll l)//(x,y)是障碍点,(a,b)是当前棋盘的左上角坐标,l是棋盘边长

初看这个问题，似乎无从下手，于是我们可以先考虑最简单的情况，既n = 2时

0 0 0 1 这时，无论公主在哪个格子，我们都可以用一块毯子填满

继续考虑n = 4的情况

我们已经知道了解决2 * 2的格子中有一个障碍的情况如何解决，因此我们可以尝试构造这种情况

首先，显然可以将4 * 4的盘面划分成4个2 * 2的小盘面，其中一块已经存在一个障碍了

而我们只需在正中间的2 * 2方格中放入一块地毯，就可以使所有小盘面都有一个障碍

于是，n = 4的情况就解决了

我们可以将n = 4时的解法可以推广到一般情况，既当n = 2 k时，我们均可以将问题划分为4个n = 2 k – 1的子问题，然后分治解决即可。

c++

#include<bits/stdc++.h>

using namespace std;
typedef long long ll;
ll x,y; //x,y表示公主坐标

int k; //表示迷宫规格

void dfs(ll x, ll y, ll a,ll b, ll l)//(x,y)是障碍点,(a,b)是当前棋盘的左上角坐标,l是棋盘边长
{
    if(l == 1) return ;//棋盘的大小是1×1,无法再继续拆分
    if(x - a  + 1<= l / 2&& y - b + 1<= l / 2)//则在左上角
    {
        printf("%lld %lld 1\n",a + l/2,b + l/2);//则需在中心放置1号地毯,这里坐标是毯子的拐角
        dfs(x,y,a,b,l/2);//递归处理左上角
        dfs(a + l/2-1 , b+ l/2    , a         , b + l/2   ,l/2);//右上角
        dfs(a + l/2   , b+ l/2 - 1, a + l/2   , b         ,l/2);//左下角   
        dfs(a + l/2   , b+ l/2    , a + l/2   , b + l/2   ,l/2);//右下角
    }
    else if(x - a  + 1 <= l / 2&& y - b + 1 > l / 2)//在右上角
    {
        printf("%lld %lld 2\n",a + l/2,b + l/2 - 1);//则需在中心放置2号地毯
        dfs(a + l/2-1,b + l/2-1,a,b,l/2);//递归处理左上角
        dfs(x,y,a,b+l/2,l/2);//右上角
        dfs(a + l/2,b+ l/2 - 1, a + l/2, b,l/2);//左下角   
        dfs(a + l/2, b+ l/2, a + l/2, b + l/2,l/2);//右下角
    }
    else if(x - a  + 1 > l / 2&& y - b + 1 <= l / 2)//左下角
    {
        printf("%lld %lld 3\n",a + l/2 - 1,b + l/2);//则需在中心放置3号地毯
        dfs(a + l/2-1,b + l/2-1,a,b,l/2);//递归处理左上角
        dfs(a+l/2-1,b+l/2,a,b+l/2,l/2);//右上角
        dfs(x,y,a+l/2,b,l/2);//左下角  
        dfs(a + l/2, b+ l/2, a + l/2, b + l/2,l/2);//右下角
    }
    else
    {
        printf("%lld %lld 4\n",a + l/2 - 1,b + l/2-1);//则需在中心放置3号地毯
        dfs(a + l/2-1,b + l/2-1,a,b,l/2);//递归处理左上角
        dfs(a+l/2-1,b+l/2,a,b+l/2,l/2);//右上角
        dfs(a+l/2,b+l/2-1,a+l/2,b,l/2);//左下角    
        dfs(x,y, a + l/2, b + l/2,l/2);//右下角
    }
}

int main()
{
    cin >> k >> x >> y;
    dfs(x,y,1,1,pow(2,k));
    return 0;
}

P1498 南蛮图腾

c++

for(int j=i;j>0;j--)a[j]^=a[j-1];//修改数组

动态生成分形图案的每一行状态,它本质上是在模拟杨辉三角（Pascal's Triangle）的生成过程，但只关心每个位置的奇偶性（用异或运算实现）。

为什么倒序更新？

假设我们有一个数组 a = [1, 1, 0, 1]，想要生成下一行：

正序更新（从左到右）：会覆盖前面的值，导致后续计算错误。
倒序更新（从右到左）：先处理高位，保留低位未修改的值，确保计算的正确性。

例如，生成杨辉三角第3行（索引从0开始）：

原数组：[1, 2, 1]（但这里只关心奇偶性，实际存储的是 [1, 0, 1]）
生成第4行时，需要从右向左更新，避免覆盖前一行数据。

c++

#include<iostream>
using namespace std;
int n,a[1030]={1};//初始化数组,第一个元素为1,其余为0

int main(){
    cin>>n;
    for(int i=0;i<1<<n;i++){//共2的n次方行
        for(int j=1;j<(1<<n)-i;j++)cout<<" ";//前导空格,1-2^n-1,1-2^n-2...
        
        for(int j=i;j>0;j--)a[j]^=a[j-1];//修改数组
        if(!(i%2))for(int j=0;j<=i;j++)cout<<(a[j]?"/\\":"  ");//奇数行,2个空格,1个0等于2个空格
        else for(int j=0;j<=i;j+=2)cout<<(a[j]?"/__\\":"    ");//偶数行,4个空格
        cout<<endl;
    }
    return 0;
}

算法1-5贪心

总结

贪心的题一般会进行排序，并且多用结构体。一般是最小最大问题

P1223 排队接水

c++

#include<bits/stdc++.h>

using namespace std;
int n;
const int N = 1010;
struct node{
    double t;
    int id;
    bool operator<(const node&W)const{
        return t < W.t;
    }
}a[N];

int wait[N];//wait[i]表示第i人的等待时间

int main()
{
    cin >> n;
    double ans = 0,time = 0;//time表示等待时间
    for(int i = 1; i <= n; i ++){
        cin >> a[i].t;
        a[i].id = i;
    }
    sort(a+1,a+1+n);
    for(int i = 1;i <= n; i ++) {
        cout << a[i].id << " ";
        time += a[i-1].t;
        wait[i] = time;//第i人的等待时间
        ans += wait[i];
    }
    cout << endl;
    printf("%.2f",ans*1.0 / n);
    return 0;
}

P1803 凌乱的yyy / 线段覆盖

这道题贪心的思路是每次选择结束时间最早的，这样能为后面留下更多的时间参赛。

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 1e6 + 10;

struct node{
    int start,endi;
    bool operator<(const node&W)const{
        return endi < W.endi;
    }
}a[N];

int n;

int main()
{
    cin >> n;
    for(int i = 0; i < n;i ++) cin >> a[i].start >> a[i].endi;
    sort(a,a+n);
    int pre = a[0].endi;//第一个结束时间最短,一定会选上
    int ans = 1;//记录方案数
    
    for(int i = 1; i < n; i ++)
    {
        if(a[i].start >= pre)
        {
            ans++;
            pre = a[i].endi;
        }
    }
    
    cout << ans << endl;
    return 0;
}

P1090合并果子

复杂度是 O(n^2)超时

sort复杂度是O(nlogn)

c++

#include<bits/stdc++.h>

using namespace std;
int n;//果子的种类数
typedef long long ll;
ll ans;


int main()
{
    cin >> n;
    vector<ll> a(n);
    for(int i = 0; i < n;i++) cin >> a[i];
    ll tmp = 0;
    while(a.size() > 1){
        sort(a.begin(),a.end());//集合排序使用迭代器，复杂度是O(nlogn)
        ll tmp = a[0] + a[1];
        a.erase(a.begin());
        a.erase(a.begin());
        ans += tmp;
        a.push_back(tmp);
    }
    cout << ans << endl;
    return 0;
}

O(n)做法

🍔 先说说：什么是堆？

堆（Heap）是一种特殊的完全二叉树，在编程里常用来做优先级排序。
有两种堆：
- 最大堆：顶端是最大的元素（默认的 priority_queue）
- 最小堆：顶端是最小的元素（我们需要的！）

🧰 c++ 默认的 priority_queue 是最大堆

🧲 想要最小堆怎么办？

我们用这个写法：

c++

priority_queue<int, vector<int>, greater<int>> q;

解释一下：

int：存放的类型
vector<int>：底层容器
greater<int>：比较函数，告诉它“小的优先”，也就是最小堆！

🪄 你可以记住这个最小堆模板：

c++

priority_queue<类型, vector<类型>, greater<类型>> 变量名;

📝 总结一下

操作	意义	举例
`push(x)`	把 `x` 放进堆里	`pq.push(5);`
`pop()`	删除堆顶元素（最小值）	`pq.pop();`
`top()`	查看堆顶元素（最小值）	`cout << pq.top();`

仅堆顶可读

贪心思路：每次选择最小的两堆进行合并

c++

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

int main() {
    int n;
    cin >> n;
    priority_queue<ll, vector<ll>, greater<ll>> pq; // 小根堆
    for (int i = 0; i < n; i++) {
        ll x;
        cin >> x;
        pq.push(x);
    }

    ll ans = 0;
    while (pq.size() > 1) {
        ll a = pq.top(); pq.pop();
        ll b = pq.top(); pq.pop();
        ll sum = a + b;
        ans += sum;
        pq.push(sum);
    }

    cout << ans << endl;
    return 0;
}

P3817 小A的糖果

如果相邻两个盒子糖果的数量大于 x，就吃右边盒子的糖，否则不进行任何操作。

为什么要吃右边盒子的糖：这是因为如果我们吃掉左边盒子里的糖，就只会减少这一轮相邻两个盒子糖果的数量；如果我们吃掉右边盒子里的糖，那么这次操作还可以减少下一轮相邻两个盒子糖果的数量，符合贪心的逻辑。

c++

#include<bits/stdc++.h>

using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
ll a[N];

int main()
{
    int n,x;
    cin >> n >> x;
    for(int i = 1; i <= n;i++) cin >> a[i];
    ll ans = 0;
    for(int i = 1; i <= n;i++) //正好利用a[0] = 0
    {
        if(a[i-1] + a[i] > x)//如果超了，则吃掉右边多余的糖果
        {
            ans += a[i-1] + a[i] - x;
            a[i] = x - a[i-1];
        }
    }
    cout << ans << endl;
    return 0;
}

P1106 删数问题

sort函数的用法

默认是从小到大排序，如果要从大到小排序，则可写成如下格式：

c++

sort(a,a+len,greater<int>());

重点是原左右次序

🧠 我们先说 string 的 erase 用法

c++

string str = "abcdef";
str.erase(pos, len);  // 从 pos的索引位置开始，删除 len 个字符

✅ 示例 3：只给一个参数，删除从这个位置到末尾

c++

string str = "abcdef";
str.erase(3); // 删除从索引3开始（含）之后的所有字符
cout << str;  // 输出 abc

🧠 vector 的 erase 用法也很类似

这里只给一个参数，只能删除给定位置索引的元素，不会删后面的

c++

vector<int> v = {1, 2, 3, 4, 5};
v.erase(v.begin() + 2); // 删除索引为 2 的元素（也就是 3）

你也可以删除一个范围：(含头不含尾)

c++

v.erase(v.begin() + 1, v.begin() + 4); // 删除 2~4（含头不含尾），结果是 {1, 5}

贪心的思想是每次删除数字中的极大值！

❓ 你想让一个数变小，怎么做？

从左到右，先比较高位！

最高位大 → 整体大
所以你想尽早删掉一个大数
如果你删的是左边的“高位的大数”，整体数就更小

所以： 从左往右找到第一个比后面大的数，删掉它，最有“贡献”！

c++

#include<bits/stdc++.h>
using namespace std;
int main(){
    string n;
    int s,i;
    cin>>n>>s;
    while(s){
        for(i=0;n[i]<=n[i+1] && i + 1 < n.size();)//找极大值
            i++;
        n.erase(i,1);//删除函数,就是从第i个位置连续删1个。如果不清楚删除函数，可以百度。
        s--;
    }
    while(n[0]=='0'&&n.size()>1){//处理前导零，注意如果长度是1就不能再删了。
        n.erase(0,1);
    }
    cout<<n;
    return 0;
}

解法二：

c++

#include<bits/stdc++.h>

using namespace std;
int a[260];
bool flag;//用来标识是否全为0

int main()
{
    string n;
    int k;
    cin >> n >> k;
    
    for(int i = 1; i <= n.size();i++) a[i] = n[i-1] - '0';
    int aim = n.size() - k,now = 0,tmp = 1,minp = 0;//tmp表示当前序列的起点
    while(now < aim)
    {
        minp = tmp;
        for(int i = tmp;i <= k + tmp;i++) if(a[minp] > a[i]) minp = i;//到k+tmp之间有k个数足够删除
        if(a[minp]) flag = true;//不为0的话
        if(flag) cout << a[minp]; //首位特判，首位非0后面则输出
        k -= minp - tmp;//表示删除了几个数
        tmp = minp + 1;//下次从选了的数后面开始
        now++;//当前选了的数加1
    }
    
    if(!flag) cout << 0;//如果一直是0的话
    
    return 0;
}

P1478 陶陶摘苹果

贪心的思路是先取花费力气少的，留下更多的力气去拿后面的。

c++

#include<bits/stdc++.h>

using namespace std;
struct node{
    int x,y;//分别是高度和力气
    bool operator<(const node&W)const{
        return y < W.y;
    }
}arr[5010];

int main()
{
    int n,s;
    cin >> n >> s;
    int a,b;
    cin >> a >> b;//椅子高度和手伸直长度
    
    if(n == 0){cout << 0; return  0;}
    
    for(int i = 0; i < n; i ++) cin >> arr[i].x >> arr[i].y;
    
    sort(arr,arr+n);
    int i = 0,sum = a + b,ans = 0;
    
    while(true)
    {
        if(arr[i].x <= sum && s >= arr[i].y){
            ans++;
            s -= arr[i].y;
        }
        else if(s < arr[i].y || s < 0) break;
        i++;
    }
    cout << ans << endl;
    return 0;
}

P5019 铺设道路

贪心的核心思想：

如果 a[i] 比 a[i-1] 大：那么我们知道从 a[i-1] 到 a[i] 之间的差就是需要额外填充的部分，因此我们加上 a[i] - a[i-1]。
如果 a[i] 比 a[i-1] 小：这个时候，我们不需要额外填充，只要关注前一个坑即可，因为当前坑已经被前一个坑的操作填补掉了。

为什么贪心是对的：

如果 a[i] 比 a[i-1] 大，直接填充当前的差值 a[i] - a[i-1]，这相当于我们处理一个新坑的深度。
如果 a[i] 比 a[i-1] 小，那么前一个坑已经处理过它并填充了这个部分，当前坑不需要额外的操作。

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 1e5 + 10;
int a[N],ans;//ans表示答案

int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++){
        cin >> a[i];
        ans += max(a[i] - a[i-1],0);//当前坑需要填的深度
    }
    cout << ans << endl;
    return 0;
}

P1208Mixing Milk

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 2e6 + 10;

struct node{
    int p,num;
    bool operator<(const node&W)const{
        return p < W.p;
    }
}a[N];

int main()
{
    int n,m;
    cin >>n >> m;
    for(int i = 0; i < m;i ++) cin >> a[i].p >> a[i].num;
    int now = 0,ans = 0;
    int i = 0,need = n;
    sort(a,a+m);

    while(now != n)
    {
        int tmp = (a[i].num >= need ? need:a[i].num);
//      cout << "tmp=" << tmp << endl;
        ans += tmp * a[i].p;
        now += tmp;
        need -= tmp;
        i++;
    }
    cout << ans << endl;
    return 0;
}

P1094 纪念品分组

我们先将数据进行排序，然后维护两个变量 x 和 y，让 x 指向开头，让 y 指向结尾。

一直循环，过程中会出现两种情况。

如果当前两个变量所指的两个数之和小于或等于 w，说明可行，就把它们两个分为一组，同时将 x 加 1，将 y 减 1，并将答案加 1，这是第一种情况。
如果当前两个变量所指的两个数之和大于 w，说明不可行，只将 y 减 1，同时答案加 1 即可，这是第二种情况。

重复以上过程，直到 x>y 时停止循环。

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 3e4 + 10;
int a[N],used[N];
int ans;

using namespace std;
int main()
{
    int w,n;
    cin >> w >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    
    sort(a+1,a+n+1);
    int i = 1, j = n;
    while(i <= j)
    {
        if(a[i] + a[j] > w) j--;
        else i++,j--;
        ans++;      
    }
    cout << ans << endl;
    return 0;
}

P4995 跳跳！

记得开long long，因为hi最大可能为1e4，平方完1e8，继续加可能爆int

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 310;
int a[N];
typedef long long ll;

int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    
    sort(a,a+n+1);
//  for(int i = 0; i <= n;i ++) cout << a[i] << ' ';
    ll ans = 0,num = 0,i = 0,j = n;
    while(i <= j){
        ans += pow(a[j] - a[i],2);//向右跳
        i++,j--;
    }
    i = 1, j = n;
    while(i <= j)
    {
        ans += pow(a[j] - a[i],2);//向左跳
        i++,j--;
    }
    cout << ans << endl;
    return 0;
}

更便捷的写法：

c++

#include<bits/stdc++.h>
using namespace std;
unsigned long long ans=0;
int h[330];
bool sum=0;
signed main()
{
    int n;
    cin>>n;
    for (int i=1;i<=n;i++) cin >> h[i];
    sort(h+1,h+n+1);
    int j=0,hpast=0; //j表示当前取的石头位置，hpast是上一次跳的石头高度
    for (int i=1;i<=n;i++)
    {
        j=n-j+sum;// 交替：n-j 是从另一边开始，+sum 是让左右交替
        sum=!sum;
        ans+=(h[j]-hpast)*(h[j]-hpast);
        hpast=h[j];
    }
    cout<<ans;
    return 0;
}

P4447 分组

在 c++ 中，map 是一个非常常用的 关联容器，定义在 <map> 头文件中。它是 STL（标准模板库） 的一部分，提供了 键值对（key-value） 的数据结构

🌟 简要定义

c++

std::map<KeyType, ValueType>

KeyType：键的类型（必须支持 < 比较）
ValueType：值的类型

map 会 自动按照 key 排序，通常是按升序排列（默认使用 < 运算符）。

🔧 常用操作

操作	示例	说明
插入	`m["key"] = value;` 或 `m.insert({key, value});`	插入或修改元素
查找	`m.find(key)`	返回迭代器，指向元素；若不存在，返回 `m.end()`
删除	`m.erase(key);`	删除指定 key 的元素
判断是否存在	`m.count(key)`	返回 0 或 1（map 不允许重复键）
大小	`m.size()`	元素个数
清空	`m.clear()`	删除所有元素

✅ 正确写法回顾

c++

std::map<int, int> m;
auto i = m.begin();
// 第一种写法（解引用 + 点）
(*i).second--;
// 第二种写法（推荐，简洁）
i->second--;

c++

#include<bits/stdc++.h>

using namespace std;

map<int,int> m;

int main()
{
    int n, ans = INT_MAX;
    cin >> n;
    for(int i = 0; i < n; i ++) {int t;cin >> t;m[t] ++;}
    
    while (!m.empty())
    {
        auto i = m.begin(), j = m.begin();  // 使用 auto推导迭代器类型
        i->second--;  // 已经画线，所以下面找递增是大于
        int t = 1;// 若 i, j 所对应的能力值是连续的，且i对应的那一列高度不高于j，则继续画线
        for (++j; j != m.end() && j->first == i->first + 1 && j->second > i->second; i++, j++) {
            t++;
            j->second--;
        }
        i = m.begin();
        while (i != m.end() && i->second == 0) m.erase(i++->first);  // 删除画完线高度为0的元素
        
        if (t < ans) ans = t;  //动态记录画线过程中的最小值
    }
    cout << ans << endl;
    
    return 0;
}

P1080 国王游戏

**ans1是最高位,**高位在前,低位在后

**p1是最高位,**高位在前,低位在后

sum1 是最低位，低位在前，高位在后

✅ 对比总结一下

数组	用途	低位	高位
`sum`	当前正在参与计算的数（参与乘法和除法）	`sum[1]`	`sum[m]`
`ans`	每次除法的结果	`ans[ls]`	`ans[1]`
`p`	最终记录的最大结果	`p[lp]`	`p[1]`

所以这份代码内部其实用了两种顺序：

计算时（如乘法）用“低位在前”顺序（便于进位）
结果保存/比较/输出时用“高位在前”顺序（符合人类习惯）

c++

#include <bits/stdc++.h>
using namespace std;

int n, a, b, m;             // m 表示 sum 的有效位最大下标
int p[1010], lp = 0;        // p 存当前最大值结果，高精度整数，lp 是最大下标
int sum[1010];              // sum 存当前乘积，高精度整数
int ans[1010], ls = 0;      // ans 存除法结果临时数组，ls 是最大下标
int res;                    // 除法中保存的余数

struct node {
    int a, b;
    bool operator<(const node &W) const {
        return a * b < W.a * W.b;
    }
} arr[1010];

bool compare() {
    int i = 0, j = 0;
    while (i <= lp && p[i] == 0) i++;  // 去除 p 的前导 0
    while (j <= ls && ans[j] == 0) j++;  // 去除 ans 的前导 0
    
    int len1 = lp - i + 1;
    int len2 = ls - j + 1;
    if (len1 > len2) return false;
    if (len1 < len2) return true;
    
    while (i <= lp && j <= ls) {
        if (p[i] < ans[j]) return true;
        if (p[i] > ans[j]) return false;
        i++;
        j++;
    }
    return false;
}

void cheng(int d) {
    for (int i = 0; i <= m; i++) sum[i] *= arr[d].a;
    for (int i = 0; i <= m; i++) {
        sum[i + 1] += sum[i] / 10000;
        sum[i] %= 10000;
    }
    if (sum[m + 1] != 0) m++;
}

void div(int d) {
    memset(ans, 0, sizeof(ans));
    ls = 0;
    while (m >= 0 && sum[m] == 0) m--;  // 去掉前导0
    res = 0;
    int flag = 0;
    for (int i = m; i >= 0; i--) {
        res = res * 10000 + sum[i];
        ans[++ls] = res / arr[d].b;
        if (ans[ls] == 0 && !flag) ls--;  // 不保留前导 0
        else flag = 1;
        res %= arr[d].b;
    }
}

int main() {
    cin >> n >> a >> b;
    for (int i = 0; i < n; i++) cin >> arr[i].a >> arr[i].b;
    sort(arr, arr + n);
    
    m = 0;
    memset(sum, 0, sizeof(sum));
    sum[0] = a;
    
    for (int i = 0; i < n; i++) {
        div(i);  // 先除
        if (compare()) {
            lp = ls;
            memcpy(p, ans, sizeof(ans));
        }
        cheng(i);  // 再乘
    }
    
    int i = 0;
    while (i <= lp && p[i] == 0) i++;  // 去前导0
    if (i > lp) {  // 全是0
        printf("0\n");
        return 0;
    }
    
    printf("%d", p[i++]);
    for (; i <= lp; i++) {
        printf("%04d", p[i]);  // 补足4位
    }
    printf("\n");
    return 0;
}

算法1-7搜索

P1135 奇怪的电梯

1. memset(dist, 0x3f, sizeof(dist)) 实际干了啥？

memset 会把内存中每个字节（byte）都设成 0x3f（也就是十进制的 63）。
而一个 int 在 c++ 中通常是 4 个字节（32 位）。

所以，每个 int 被填成：

c++

0x3f3f3f3f

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 210;
int k[N],dist[N];
int n,a,b;


void dfs(int id,int step)//id表示当前在几楼,step表示到该楼的最小步数
{
    dist[id] = step;
    int nextid = id - k[id];
    if(nextid >= 1 && step + 1 < dist[nextid]) dfs(nextid,step + 1);//下，注意剪枝
    
    nextid = id + k[id];
    if(nextid <= n && step + 1 < dist[nextid]) dfs(nextid,step + 1);//上
    return;
}

int main()
{
    memset(dist,0x3f,sizeof(dist));
    cin >> n >> a >> b;
    for(int i = 1; i <= n; i ++) cin >> k[i];
    dfs(a,0);
    if(dist[b] == 0x3f3f3f3f) cout << -1;
    else cout << dist[b];
    return 0;
}

P1219八皇后 checker challenge

c++

#include<bits/stdc++.h>

using namespace std;
int a[20][20];//棋盘
int ans;
int col[20],dg[40],udg[40];
int n;
int path[20];

void dfs(int id)//当前在考虑第几行
{
    if(id == n + 1)
    {
        ans++;
        if(ans <= 3) {
            for(int i = 1; i <= n;i++) cout << path[i] << " ";
            cout << endl;
        }
    }
    
    for(int i = 1; i <= n; i ++) //考虑id行i列
    {
        if(!col[i] && !dg[id + i] && !udg[i - id + n])
        {
            col[i] = dg[id + i] = udg[i - id + n] = 1;
            path[id] = i;
            dfs(id + 1);
            col[i] = dg[id + i] = udg[i - id + n] = 0;
        }
    }
}

int main()
{
    cin >> n;
    
    dfs(1);
    cout << ans;
    return 0;
}

P1443 马的遍历

✅ 宽度优先搜索（BFS）特别适合用来找“无权图”的最短路！

🧠 为什么？

因为 BFS 是一层一层扩展的，它保证了：

第一次到达某个点的时候，所走的步数就是最短的。

c++

#include<bits/stdc++.h>

# define PII pair<int,int>
using namespace std;

queue<PII> q;//queue是先进先出
int f[410][410];//存到某点的最短步数
bool vis[410][410];//保存是否走过

int dx[8] = {-2,-1,1,2, 2, 1,-1,-2};
int dy[8] = { 1, 2,2,1,-1,-2,-2,-1};
int n,m,x,y;

int main()
{
    cin >> n >> m >> x >> y;
    memset(f,-1,sizeof(f));
    memset(vis,false,sizeof(vis));
    
    f[x][y] = 0;
    vis[x][y] = true;
    q.push({x,y});
    
    while(!q.empty())
    {
        int xi = q.front().first,yi = q.front().second;
        q.pop();
        for(int i = 0; i < 8; i ++){
            int u = xi + dx[i], v = yi + dy[i];
            if(u < 1 || u > n || v < 1 || v > m || vis[u][v]) continue;
            vis[u][v] = true;
            q.push({u,v});
            f[u][v] = f[xi][yi] + 1;
        }
    }
    for(int i = 1; i <= n;i++){
        for(int j = 1; j <= m; j ++) cout << f[i][j] << " ";
        cout << endl;
    }
        
    return 0;
}

dfs结果超时

c++

#include<bits/stdc++.h>

using namespace std;
int path[410][410];//表示最短距离

int px[8] = {-2,-1,1,2, 2, 1,-1,-2};
int py[8] = { 1, 2,2,1,-1,-2,-2,-1};
int n,m,x,y;

bool iscan(int x,int y)
{
    if(x < 1 || x > n || y < 1 || y > m) return false;
    return true;
}

void dfs(int xi,int yi,int step)//表示当前所在的位置,以及到该点用了几步
{
    path[xi][yi] = step;
    for(int i = 0; i < 8;i++)
    {
        if(iscan(xi+px[i],yi+py[i]) && step + 1 < path[xi + px[i]][yi+py[i]]) 
            dfs(xi + px[i],yi+py[i],step + 1);
    }
    return ;
}

int main()
{
    memset(path,0x3f,sizeof(path));
    cin >> n >> m >> x >> y;
    dfs(x,y,0);
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= m;j++) 
        {
            if(path[i][j] == 0x3f3f3f3f) cout << -1 << " ";
            else cout << path[i][j] << " ";
        }
        cout << endl;
    }
        
    
    return 0;
}

P2895 Meteor Shower S

✅ 那为什么 BFS 要判断“有没有走过”呢？

因为——

BFS 是一层一层地找最短路的，如果一个点你已经访问过，说明你之前已经用更短的时间走到它了！现在再来一次，就是浪费时间，还可能是“更慢的路径”。

c++

#include<bits/stdc++.h>

using namespace std;
#define PII pair<int,int>
int n;
int a[310][310];//记录陨石砸落时间
int vis[310][310];//记录是否走过
int x,y,t;//陨石坐标，砸落时间
int dist[310][310]; //记录到达某点的最短时间

int dx[5]={0,0,0,1,-1};//方便移动和处理陨石砸落
int dy[5]={0,1,-1,0,0};

int ch(int x){//判断路过该点时是否陨石已经砸落，如果是没有陨石，相当于n年后砸落
    if (x==-1) return 99999;
    else return x;
}

void sign(int i,int t)//标记陨石的下落时间
{
    if(x + dx[i] >= 0 && y + dy[i] >= 0 && (a[x + dx[i]][y + dy[i]] == -1 || a[x + dx[i]][y + dy[i]] > t))
        a[x + dx[i]][y + dy[i]] = t;
}

int main()
{
    cin >> n;
    memset(a,-1,sizeof(a));//陨石砸落时间初始化
    for(int i = 1; i <= n; i++){
        cin >> x >> y >> t;
        for(int i = 0; i < 5; i ++) sign(i,t);
    }
    
    queue<PII> q;
    vis[0][0] = true;
    q.push({0,0});
    while(!q.empty())
    {
        int x = q.front().first,y = q.front().second;
        q.pop();
        int s = dist[x][y] + 1;//下一格子到达的时间等于当前格子加1
        if(a[x][y] == -1){
            cout << s - 1;
            return 0;
        }
        for(int i = 1; i <= 4; i ++)
        {
            int xi = x + dx[i],yi = y + dy[i];
            if(xi >= 0 && yi >= 0 && s < ch(a[xi][yi]) && vis[xi][yi] == 0)//在边界内
            //且下一时刻陨石没下楼且没被访问
            {
                q.push({xi,yi});
                vis[xi][yi] = 1;
                dist[xi][yi] = s;
            }
        }
    }
    cout << -1 << endl;
    return 0;
}

算法2-1前缀和、差分与离散化

P8218 求区间和

c++

#include<bits/stdc++.h>

using namespace std;
const int N = 1e5 + 10;
int a[N];

int main()
{
    int n,m;
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i],a[i] += a[i-1];//a[i]表示的是截止到i为止的和
    cin >> m;
    for(int i = 0; i < m;i++)
    {
        int c,d;
        cin >> c >> d;
        cout << a[d] - a[c-1] << endl;
    }
    return 0;
}

动态规划1

P2196 挖地雷

暴力DFS写法

c++

#include<bits/stdc++.h>

using namespace std;
int a[30][30];//表示地窖之间的连接情况,1表示有连接
int path[30],ans;//存放最终结果的路径数组,最终的地雷数
int tempath[30],temp;//中间变量
int used[30];//是否用过
int passby;//表示走过的地窖数
int pass_ans;//表示最终走过的地窖数

int n;//表示地窖数
int num[30];//表示地窖内的地雷数组

bool isconnect(int id)//判断是否还有路径
{
    for(int i = 1;i <= n;i++)
        if(a[id][i] && !used[i]) return true;
    return false;
}

void dfs(int id)//当前准备进入的地窖是id号地窖
{
    if(!isconnect(id)) //没连接返回
    {
        if(temp > ans)//找到了更多地雷的方案
        {
            ans = temp;
            pass_ans = passby;
            for(int i = 1; i <= passby;i++) path[i] = tempath[i];
        }
        return ;
    }
    
    for(int i = 1; i <= n;i++)
    {
        if(a[id][i] && !used[i])
        {
            used[i] = 1;//该地窖走过了
            passby++;//走过的地窖数➕➕
            tempath[passby] = i;
            temp += num[i];
            
            dfs(i);//去该地窖
            
            used[i] = 0;
            tempath[passby] = 0;
            passby--;
            temp -= num[i];
        }
    }
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n;i++) cin >> num[i];
    for(int i = 1; i <= n - 1;i++)//共n-1行
    {
        int index = i + 1,t;
        for(int j = 1; j <= n - i;j++) {cin >> t; a[i][index] = t;
            index++;
        }   
    }
        
    for(int i = 1; i <= n;i++)//因为起点不一定是1,所以每个起点都遍历一下
    {
        used[i] = 1;
        passby = 0;
        tempath[++passby] = i;
        temp += num[i];
        dfs(i);
        temp -= num[i];
        used[i] = 0;
        
    }
    for(int i = 1; i <= pass_ans;i++) cout << path[i] << " ";
    cout << endl << ans<< endl;
    return 0;
}

Ac贪心:

memcpy 的正确用法是：

c++

void *memcpy(void *dest, const void *src, size_t n);

也就是：

c++

memcpy(目标地址, 源地址, 拷贝的字节数);

2025蓝桥杯突击训练